$ \DeclareMathOperator{\sen}{sen} \newcommand{\R}{\mathbb{R}} \newcommand{\vt}[1]{\vec{\textbf{#1}}} \newcommand{\vtu}[1]{\hat{\textbf{#1}}} \newcommand{\rot}{\text{Rot}} $ O objetivo deste post é demonstrar as seguintes igualdades:

\[\sen(\alpha+\beta)=\sen(\alpha)\cos(\beta)+\sen(\beta)\cos(\alpha)\] \[\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sen(\alpha)\sen(\beta)\]

Um vetor $\vt{v}=(\color{red}{a},\,\color{blue}{b})\in\R^2$ pode ser representado através da combinação linear da base cartesiana:

\[\vt{v}=\color{red}{a}\vtu{x}+\color{blue}{b}\vtu{y}\]

Além disso, uma rotação de $\theta$ unidades da base cartesiana na circunferência unitária é dada por:

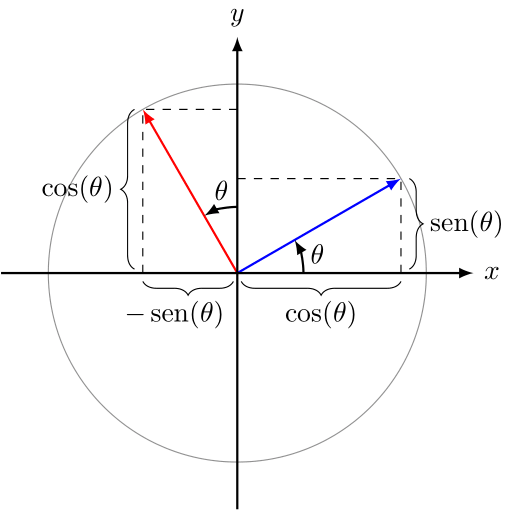
Esquematização de uma rotação da base cartesiana R^2

\[\rot_\theta(\vtu{x})= \begin{bmatrix} \cos(\theta)\\ \sen(\theta) \end{bmatrix} \quad\text{ e }\quad \rot_\theta(\vtu{y})= \begin{bmatrix} -\sen(\theta)\\ \cos(\theta) \end{bmatrix}\]

A rotação no plano preserva algumas propriedades úteis. Com $k$ e $\theta\in\R$, um vetor $\vt{v}$ rotacionado por $\theta$ e depois escalonado por $k$ é o mesmo que um vetor $\vt{v}$ escalonado por $k$ e depois rotacionado por $\theta$.

\[k\rot_\theta(\vt{v})=\rot_\theta(k\vt{v})\]

Isso significa um vetor $\vt{v}$ pode ser pensado como a base cartesiana rotacionada e escalonada pelas componentes de $\vt{v}$:

\[\begin{align*} \rot_\theta(\vt{v})&=\color{red}{a}\rot_\theta(\vtu{x})+\color{blue}{b}\rot_\theta(\vtu{y})\\ &= \color{red}{a} \begin{bmatrix} \cos(\theta)\\ \sen(\theta) \end{bmatrix} + \color{blue}{b} \begin{bmatrix} -\sen(\theta)\\ \cos(\theta) \end{bmatrix}\\ &= \tag{1}\label{equacao-rocatao-vetor} \begin{bmatrix} \color{red}{a}\cos(\theta)-\color{blue}{b}\sen(\theta)\\ \color{red}{a}\sen(\theta)+\color{blue}{b}\cos(\theta) \end{bmatrix} \end{align*}\]

A sacada é que a equação (\ref{equacao-rocatao-vetor}) também pode ser aplicada em um vetor que já foi rotacionado. Por exemplo, ao rotacionar $\vtu{x}$ primeiramente por $\alpha$ e depois por $\beta$, teremos o mesmo resultado se tivéssemos rotacionado por $\beta$ e depois por $\alpha$. O resultante dessas rotações sucessivas é justamente a aplicação da rotação $\alpha+\beta$ em $\vtu{x}$:

\[\rot_{\alpha+\beta}(\vtu{x})=\rot_\alpha(\rot_\beta(\vtu{x}))=\rot_\beta(\rot_\alpha(\vtu{x}))\]

Agora, para demonstrar o que foi proposto, considere um vetor $\vt{u}$ como $\rot_\alpha(\vtu{x})$. Suas componentes são o vetor $\vtu{x}$ rotacionado em $\alpha$ unidades, isto é, são $(\cos\alpha,\,\sen\alpha)$. Se rotacionarmos $\vt{u}$ em $\beta$ unidades, teremos aplicado uma rotação total de $\alpha+\beta$ unidades no vetor inicial $\vtu{x}$. Então, basta tomar $\color{red}a=\cos(\alpha)$ e $\color{blue}b=\sen(\alpha)$ na equação (\ref{equacao-rocatao-vetor}) e rotacionar $\vt{u}$ em $\beta$ unidades:

\[\begin{align*} \rot_\beta(\vt{u})&=\rot_\beta(\rot_\alpha(\vtu{x}))\\ &= \rot_\beta\left( \begin{bmatrix} \cos(\alpha)\\ \sen(\alpha) \end{bmatrix} \right)\\ &= \begin{bmatrix} \color{red}{\cos(\alpha)}\cos(\beta)-\color{blue}{\sen(\alpha)}\sen(\beta)\\ \color{red}{\cos(\alpha)}\sen(\beta)+\color{blue}{\sen(\alpha)}\cos(\beta) \end{bmatrix}\\ &= \begin{bmatrix} \cos(\alpha+\beta)\\ \sen(\alpha+\beta) \end{bmatrix} \end{align*}\]