Como desenhar um polígono regular com LaTeX e TikZ?
Um polígono regular é um polígono que possui $n$ (com $n\geq3$) lados com mesmo comprimento e também ângulos internos iguais (congruentes). Para conseguirmos desenhar um polígono regular, precisamos lembrar de uma informação importante:
📝 Todo polígono regular está inscrito (dentro) em uma circunferência.
Isto é, todos os seus vértices estão na circunferência e sempre a uma distância $r$, que é o próprio raio da circunferência. Veja alguns casos:
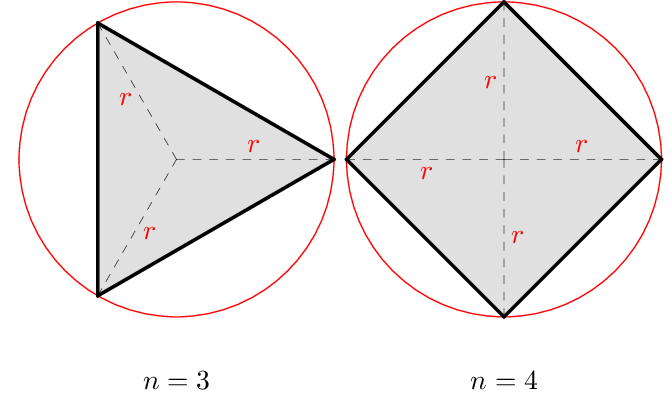
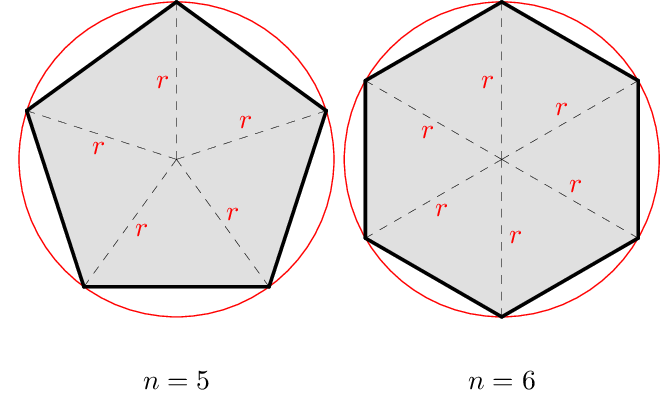
A ideia deste post é: vamos criar um comando/macro em $\LaTeX$ com TikZ para desenhar um polígono regular. Vamos fazer isso de forma parametrizada a partir do número de lados $n$, inicialmente.
Eu costumo utilizar o Overleaf para escrever documentos com $\LaTeX$, mas você pode utilizar outro de sua preferência.
Após criar o projeto, podemos estruturar um documento mínimo para criação da nossa figura de interesse:
\documentclass{standalone}
% pacote 'tikz' para criar desenhos
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
% conteúdo
\end{tikzpicture}
\end{document}
Ao utilizar o tipo de documento standalone, vamos obter um PDF que conterá somente a imagem, sem bordas desnecessárias. Importando o pacote tikz, conseguimos utilizar o ambiente tikzpicture para colocar nossos comandos de desenho.
Pensando nas formas de escrita de um ponto disponíveis no pacote tikz, vale mais a pena trabalharmos na representação polar. Na representação polar de um ponto, precisamos de apenas duas informações: o raio $r$ da circunferência e do ângulo $\alpha$ em relação ao eixo $x$. Veja a ilustração de dois pontos ${\color{blue}{A=(r,\,\alpha)}}$ e ${\color{red}{B=(r,\,\beta)}}$ quaisquer:
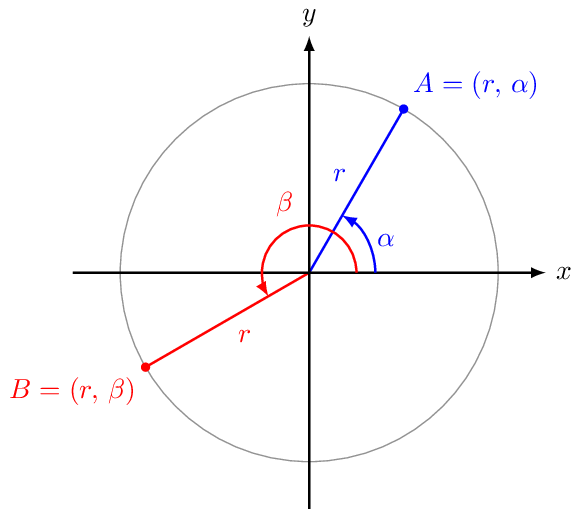
Como todos os vértices do polígono regular sempre estão $r$ unidades da origem, basta encontrarmos o valor do ângulo de cada vértice. Para sabermos o valor do ângulo de cada vértice do polígono regular, precisamos calcular o valor do ângulo central $\alpha$ da circunferência em função do número de lados $n$ do polígono. Isto é, é direto que $\alpha=\frac{360^\circ}{n}$. Note que múltiplos de $\alpha$ estão igualmente espaçados ao longo de toda a circunferência.
Por exemplo, a partir $r$ e de $\alpha$, os três pontos que formam o triângulo equilátero são, para $\alpha=\frac{360^\circ}{3}=120^\circ$:
\[\begin{align*} P_1&=(r,\,1\cdot\alpha)=(r,\,1\cdot120^\circ)=(r,\,120^\circ)\\ P_2&=(r,\,2\cdot\alpha)=(r,\,2\cdot120^\circ)=(r,\,240^\circ)\\ P_3&=(r,\,3\cdot\alpha)=(r,\,3\cdot120^\circ)=(r,\,360^\circ) \end{align*}\]Da mesma maneira, os quatro pontos que formam o quadrado são, para $\alpha=\frac{360^\circ}{4}=90^\circ$:
\[\begin{align*} P_1&=(r,\,1\cdot\alpha)=(r,\,1\cdot90^\circ)=(r,\,90^\circ)\\ P_2&=(r,\,2\cdot\alpha)=(r,\,2\cdot90^\circ)=(r,\,180^\circ)\\ P_3&=(r,\,3\cdot\alpha)=(r,\,3\cdot90^\circ)=(r,\,270^\circ)\\ P_4&=(r,\,4\cdot\alpha)=(r,\,4\cdot90^\circ)=(r,\,360^\circ) \end{align*}\]📝 Note que essa atribuição de pontos faz sempre o $n$-ésimo (último) ponto ficar sempre com ângulo de ${360^\circ}$, independentemente do valor escolhido para $n$.
Assim, para desenhar o polígono precisamos apenas conectar o ponto $P_i$ com o seu próximo $P_{i+1}$. Conectar o $i$-ésimo com o $(i+1)$-ésimo ponto funciona mesmo quando $i=n$, pois o ângulo do ponto $(n+1)$ é igual ao ângulo do primeiro ponto, pela estrutura cíclica dos ângulos na circunferência.
Vamos realizar a conexão dos pontos com um segmento de reta através de alguma estrutura iterativa. A estrutura iterativa que vamos utilizar é uma bem conhecida em qualquer linguagem de programação: o foreach (para cada). Mas antes de montá-lo, é interessante sabermos como criar variáveis dentro do ambiente tikzpicture:
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\pgfmathsetmacro{\n}{3} % lados do polígono
\pgfmathsetmacro{\r}{2} % raio da circunferência circunscrita
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
\end{tikzpicture}
\end{document}
Conseguimos criar uma variável com o macro \pgfmathsetmacro{identificador}{valor}. Criamos duas variáveis que precisaremos para desenhar o antiprisma: $n$ e $r$, mas com valores chumbados que vamos parametrizar depois. Foi criada também uma terceira variável $a$ para guardar o valor do ângulo central, a partir de $n$.
Com isso, ao utilizar o foreach já conseguimos desenhar um polígono regular. Fique à vontade para mudar o valor de $n$ e ver como ele impacta na construção da figura.
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\pgfmathsetmacro{\n}{3} % lados do polígono
\pgfmathsetmacro{\r}{2} % raio da circunferência circunscrita
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw ({\i*\a}:\r) -- ({(\i+1)*\a}:\r);
}
\end{tikzpicture}
\end{document}
Utilizamos o comando \draw para desenhar os segmentos de reta para conectar $P_i$ com $P_{i+1}$. Veja que as coordenadas foram escritas no formato polar $(\alpha:r)$ do tikz, que produz a seguinte figura:
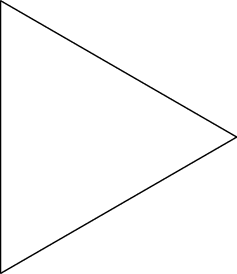
Podemos numerar cada vértice do polígono gerado. Basta adicionar um node para cada segmento:
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\pgfmathsetmacro{\n}{3} % lados do polígono
\pgfmathsetmacro{\r}{2} % raio da circunferência circunscrita
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
}
\end{tikzpicture}
\end{document}
Que gera o seguinte resultado:
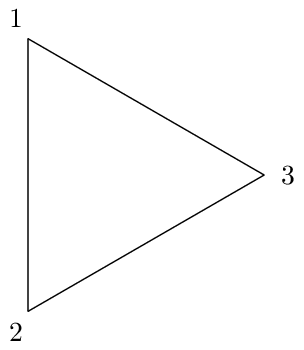
Veja que desenhamos o segmento de reta que conecta $P_i$ com $P_{i+1}$ e posicionamos o número do vértice próximo de $P_i$. Nesse processo adicionamos um pequeno valor ao raio para que o número do vértice não fique no mesmo lugar de $P_i$.
Temos o que é necessário para transformar o código acima em um comando de desenho. A ideia é deixar o valor $n$ e o raio $r$ parametrizados. Vamos criar um comando que aceita dois parâmetros. Para isso, crie um novo arquivo dentro do projeto chamado polígono-regular.tex com a seguinte estrutura base:
\newcommand{\desenharPoligonoRegular}[2]
{
% conteúdo do comando
}
Um comando com dois parâmetros em $\LaTeX$ é criado com o macro \newcommand{\nomeComando}[número de parâmetros]{}. Vamos copiar o código feito até aqui que desenha o polígono regular e fazer algumas alterações: vamos substituir onde estava $n$ e $r$ por #1 e #2, respectivamente:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
}
\end{tikzpicture}
}
Com o código acima em um arquivo separado, podemos deixar apenas a invocação do comando no arquivo principal:
\documentclass{standalone}
\usepackage{tikz}
% importação do arquivo que contém a definição do comando
\input{polígono-regular}
\begin{document}
% utilização do comando
\desenharPoligonoRegular{3}{2}
\end{document}
Perceba que importamos o arquivo contendo o comando criado com \input{polígono-regular} no preâmbulo do documento. Isso avisa o compilador que o comando definido no arquivo está disponível. Ao usar o comando \desenharPoligonoRegular{3}{2} estamos rodando o código para desenhar o polígono regular com $n=3$ e $r=2$. A imagem gerada não sofrerá alterações. Se testarmos alguns valores de $n$, teremos os seguintes resultados:
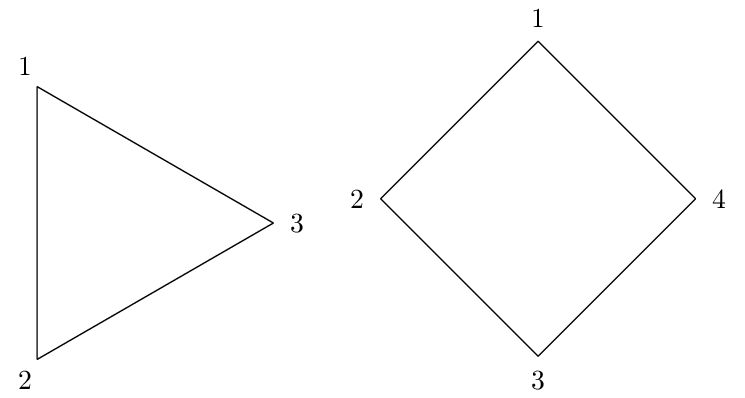
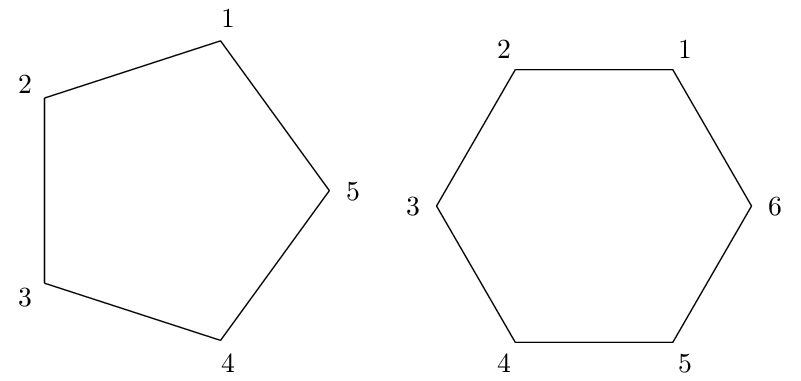
Perceba também que todos os polígonos ficaram com o primeiro vértice em $\alpha$ e o último em $360^\circ$, fazendo parecer que para alguns valores de $n$ a figura está torta. Para consertar isso, podemos utilizar o ambiente scope dentro do ambiente tikzpicture para "rotacionar a base cartesiana" em uma certa quantidade de graus sem precisar mudar as coordenadas dos vértices que escrevemos. A quantidade a ser rotacionada claramente depende de $n$, mas a pergunta que fica é: quanto rotacionar?.
Para deixar sempre o primeiro vértice do polígono fixo em, por exemplo, $90^\circ$, basta rotacionarmos a base cartesiana no ângulo complementar de $\alpha$, isto é, em $90^\circ-\alpha$:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
% criando um escopo que rotaciona a base xy cartesiana em
% 90-\a graus no sentido anti-horário
\begin{scope}[rotate=90-\a]
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
}
\end{scope}
\end{tikzpicture}
}
Que produz as seguintes figuras para alguns valores de $n$:
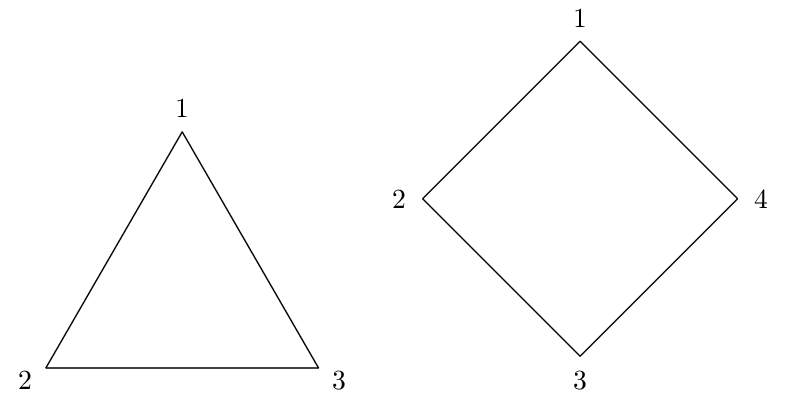

A ideia central do post está concluída, que era de mostrar como desenhar um polígono regular com $\LaTeX$ e TikZ. Entretanto, podemos ir um pouco além e adicionar mais elementos na figura, como nas primeiras deste post. O que elas têm a mais é a adição de uma circunferência circunscrita ao polígono de interesse, a conexão dos vértices do polígono ao centro dessa mesma circunferência de forma estilizada (tracejada e com um node) e uma cor de fundo. Primeiro, precisamos desenhar uma circunferência de raio $r$ antes do trecho de código que desenha os lados do polígono:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita à base
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
% circunferência circunscrita
\draw[red] (0,0) circle (\r);
% criando um escopo que rotaciona a base xy cartesiana em
% 90-\a graus no sentido anti-horário
\begin{scope}[rotate=90-\a]
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw[thick] ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
}
\end{scope}
\end{tikzpicture}
}
Além da circunferência, veja que também colocamos a opção thick nos lados do polígono para deixar seus segmentos mais grossos. Com isso, temos o seguinte resultado para $n=3$:
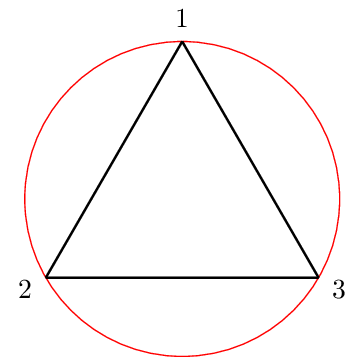
Agora, podemos conectar o vértice $P_i$ com a origem $(0,\,0)$ com um segmento de reta tracejado e bem fino dentro do foreach:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita à base
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
% circunferência circunscrita
\draw[red] (0,0) circle (\r);
% criando um escopo que rotaciona a base xy cartesiana em
% 90-\a graus no sentido anti-horário
\begin{scope}[rotate=90-\a]
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw[thick] ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
% conectando P_i com a origem
\draw[dashed, ultra thin] ({\i*\a}:\r) -- (0,0);
}
\end{scope}
\end{tikzpicture}
}
Que produz a seguinte figura para $n=3$:
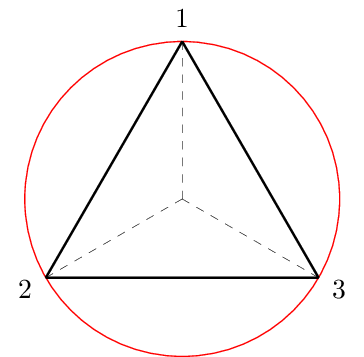
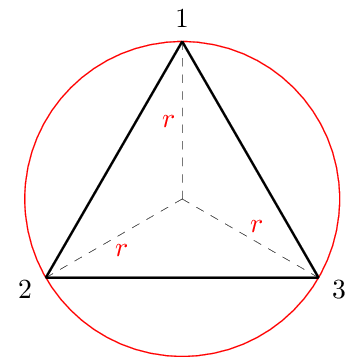
Para desenhar o texto $r$ em vermelho, fiz o seguinte: dentro de um scope rotacionando a base cartesiana em $10^\circ$, usei o comando \node posicionado na metade do valor de $r$ e mesmo ângulo $\alpha$:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita à base
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
% circunferência circunscrita
\draw[red] (0,0) circle (\r);
% criando um escopo que rotaciona a base xy cartesiana em
% 90-\a graus no sentido anti-horário
\begin{scope}[rotate=90-\a]
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw[thick] ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
% conectando P_i com a origem
\draw[dashed, ultra thin] ({\i*\a}:\r) -- (0,0);
% desenhar o texto $r$ posicionado
% na metade do valor de \r
\begin{scope}[rotate=10]
\node[red] at ({\i*\a}:\r*0.5) {$r$};
\end{scope}
}
\end{scope}
\end{tikzpicture}
}
Que produz a figura a seguir para $n=3$:
Por fim, podemos adicionar uma cor de fundo no polígono. Podemos fazer isso também via foreach, mas com uma pequena modificação. Como a ordem dos elementos desenhados importa, precisamos adicionar o trecho de código de modo que a cor de fundo seja desenhada primeiro, antes dos outros elementos:
\newcommand{\desenharPoligonoRegular}[2]
{
\begin{tikzpicture}
\pgfmathsetmacro{\n}{#1} % lados do polígono
\pgfmathsetmacro{\r}{#2} % raio da circunferência circunscrita à base
\pgfmathsetmacro{\a}{360/\n} % ângulo central a partir de '\n'
% circunferência circunscrita
\draw[red] (0,0) circle (\r);
% criando um escopo que rotaciona a base xy cartesiana em
% 90-\a graus no sentido anti-horário
\begin{scope}[rotate=90-\a]
% cor de fundo para o polígono
\fill[gray!30] (\a:\r) foreach \i in {2,3,...,\n}
{
-- ({\i*\a}:\r)
} -- cycle;
\foreach \i in {1,...,\n} % lista que vai de 1 até '\n'
{
% conectando P_i com P_{i+1}
\draw[thick] ({\i*\a}:\r) -- ({(\i+1)*\a}:\r) node at ({\i*\a}:{\r+0.3}) {\i};
% conectando P_i com a origem
\draw[dashed, ultra thin] ({\i*\a}:\r) -- (0,0);
% desenhar o texto $r$ posicionado
% na metade do valor de \r
\begin{scope}[rotate=10]
\node[red] at ({\i*\a}:\r*0.5) {$r$};
\end{scope}
}
\end{scope}
\end{tikzpicture}
}
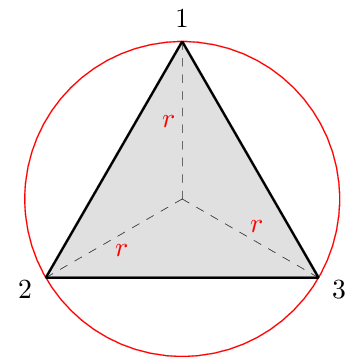
Acima, veja que usamos o comando \fill[gray!30] seguido do primeiro vértice (\a:\r). Especificamos a cor de fundo sendo um cinza $30\%$. Em seguida usamos o comando foreach, de forma a ter dentro dele as coordenadas que definem os vértices do polígono que será preenchido (de forma iterativa), da segunda em diante. Logo após o foreach, colocamos `--` cycle para fechar o polígono da cor de fundo, conectando o último vértice da iteração com o primeiro (\a:\r).
Produzindo a seguinte figura para $n=3$:
O código do projeto está disponível aqui. Agora é com você! 👋